1. Mission

In this project, we implemented of a distributed consensus protocol in the sleepy model for pedagogical use. In the sleepy consensus protocol, we adopt a leader election to refrain from the computing resources’ waste of the core idea behind Nakamoto’s blockchain protocol“proofs-of-work”, with static corruption and synchronized clocks. The Adversary could control all corrupted nodes and have the ability to delay messages up to \(\Delta\) time. The corrupted nodes hack the blockchain network with selfish mining and consistency attack. Finally, we will see that without the majority of the honest nodes, the properties consistency and quality of the blockchain can’t be guaranteed.

2. Our Team

Framework	Honest	Adversary	Integrator
Lequn Chen	Wanquan Wu *	Haoming Lu	Zihao Ye
Bicheng Gao	Ziqi Zeng *	Yuhao Zhou	Xueyuan Zhao
Songyu Ke	Yi Jiang	Xuan Zhang	Yunqi Li
Shichao Xu	Zhendong Xue	Cheng Wan	Zhi Qiu

Most of us are from Shanghai Jiao Tong University. Two of us * are from Huazhong University of Science and Technology.

3. Distributed Consensus

3.1. Introduction

First, we will talk about distributed consensus. In a distributed system, there are some rules that every node should follow. Honest nodes will behave according to those rules, while the corrupted nodes won’t. Under the interference of corrupted nodes, we want all honest nodes to reach some kind of consensus.

3.1.1. Background

The story starts from the Byzantine Generals’ Problem. Byzantine is now located in Istanbul, Turkey, which is the capital of the Eastern Roman Empire. Because at that time the Byzantine Roman Empire was vast, for the purpose of defense, each army is very far apart. The generals can only rely on the message sent by postmen to communicate with each other. At the time of the war, all the generals in the Byzantine army should reach a consensus whether to attack or not. But there may have traitors in the arm. At this time, in the case of known members of the rebellion, the remaining loyal generals to reach a consensus agreement without the influence of the traitors is the key to this problem.

In a distributed system, usually our goal is to reach Byzantine Agreement. There may have some corrupted nodes controlled by the force of evil. Nodes exchange messages through a pairwise link. At the beginning, a sender node will send messages to other nodes. If the sender is honest, it will send the same message to everyone. Otherwise, things become more complicated. Later on, every node sends the message it received to its neighboring nodes. Finally, we want all honest node to reach an agreement, which means all honest nodes have the same output. Moreover, if the sender is honest, then everyone outputs the message it received from the sender.

3.1.2. Consensus

Consensus protocols are the most critical research object of distributed computing. A dream consensus protocol will realize a “linearly ordered log” abstraction, which often referred to as state machine replication in distributed systems literature. Simply speaking, every node maintains an ever-growing ordered log of transactions. The log should satisfy two properties:

• Consistency

  At any time, all honest nodes have consistent logs(For any two honest nodes, either their logs are the same, or one log is the prefix of another). And each log should be self-consistent.
• Liveness

  If some honest node receives a transaction tx as input, or if tx appears in some honest node’s output log, then tx will appear in every other participant’s log within some fixed(small) amount of time.

3.1.3. Permission and Permissionless

Distributed systems have been analyzed historically in a permissioned setting. In a this situation, everyone knows the number of the participants in the system. And the communication channels among nodes are authenticated.

With the development of peer-to-peer system, eventually, people getting interested to the permissionless system. In this case, every node is uncertained about the exact number of participants. Anyone can join the protocol execution without geting permission from a centralized or distributed authority. Moreover, the communication channels are unauthenticated.

The difficulty of achieving permissionless consensus is from the existence of so-called “Sybil attack”, which can be easily implemented by spawning lots of nodes so it can control the majority of the nodes.

3.2. Nakamoto’s Blockchain

3.2.1. Protocol Description

In Nakamoto’s Blockchain model, every node maintains a \(\mathsf{chain}\). When a node receives a \(\mathsf{chain}\) that is valid, it will update the chain in the following way:

if |chain'| > |chain|:
    chain := chain'
    broadcast chain

3.2.2. Proof of work

In every round of an execution with security parameter \(\mathcal{K}\), we assume all nodes have access to a random function \(H:\{0 , 1\} ^* \rightarrow \{0, 1\}^\mathcal{K}\). Let \(TXs\) be the set of transactions in view but not appearing in \(\mathsf{chain}[:-T]\).

eta := random 0/1-bit string of length kappa
if H(chain, TXs, eta) < D:
    chain := concatenate(chain, TXs, eta)
    broadcast chain

For our timestamp network, we implement the proof-of-work by incrementing \(\eta\) in the block until a value is found that satisfies the corresponding hash function is less than a certain threshold \(D\).

3.2.3. Security

A blockchain protocol should satisfy chain growth, chain quality, and consistency.

• Chain growth

  Honest nodes’ chains grow steadily, neither too fast nor too slow.
• Chain quality

  In any honest node’s chain, any sufficiently long window of consecutive blocks contain a certain fraction of blocks that are mined by honest nodes.
• Consistency

  Except for \(e^{-\Omega(T)}\) fraction of execution traces, let \(\mathsf{chain}_i^r\), \(\mathsf{chain}_j^{r'}\) denote honest node \(i\) and \(j\)’s chains in round \(r\) and \(r'\) where \(r'>r\), then \(\mathsf{chain}_i^r[:-T] \prec \mathsf{chain}_j^{r'}\).

3.2.4. Attack Methods

One famous adversarial algorithm is called selfish mining, which means when a corrupt node mines a block, it doesn’t release its private chain immediately. Instead, it withholds its private chain until it observes some honest node has mined a chain of the equal enough. Then it releases private chain ahead of honest nodes, wasting the mining power of honest nodes.

4. Sleepy Consensus

4.1. Problem Set

Before we talk about the protocol, we firstly show the following assumptions:

• Synchronized clocks

  We assume that all nodes can access a globally synchronized clock that ticks over time. Each clock tick is referred as an atomic time step. Nodes can perform unbounded polynomial amount of computation in each time step, as well as receive and send polynomially many messages.
• Public-key infrastructure

  We assume that there exists a public-key infrastructure(PKI). More specifically, we shall assume that the PKI is an ideal functionality \(F_{CA}\)(only available to the current protocol instance) that does the following:

  • On receiving register(pk) from \(P\), remember the pair \((\)pk\(, P)\) and ignore any future message from \(P\).
  • On receiving lookup(\(P\)): return the store pk or \(\perp\) if not found.

• Network delivery

  The adversary controls the message delivery between nodes. We assume that the adversary can arbitrarily delay and reorder messages, as long as all the messages sent from honest nodes are received by all honest nodes within \(\Delta\) time steps.
• Static Corruptions

  We assume that once our protocol starts to run, environment can not corrupt an honest node and the corrupt node can not become an honest node.

4.2. Protocol Description

In distributed computing, typically we consider two types of nodeshonest nodes and corrupted nodes. We implemented a distributed consensus protocol in the sleepy model, which assumes that a \(majority\) of the nodes are honest. It significantly departs from key ideas behind Nakamoto’s blockchain protocol the needs for “proofs-of-work”. The protocol relies on Public-Key-Infrastructure(PKI) and all nodes are assumed to have synchronized clocks.

As showed by Pass and Shi [PS16] . One target of sleepy consensus protocol is to remove the proof-of-work from the Nakamoto blockchain while maintaining provable guarantees. To remove the proof-of-work from Nakamoto’s protocol, we make the following changes: we define the puzzle solution to be the form of \((P, t)\) instead of rate limiting through computational power, where \(P\) is the player’s identifier and \(t\) is the block-time. The pair \((P, t)\) is a “valid puzzle solution” if \(H(P,t) < D_p\) where \(H\) denotes a pseudorandom function with a common reference string and \(D_p\) is a parameter such that the has outcome is only smaller than \(D_p\) with probability \(p\). If \(H(P,t) < D_p\) we say that \(P\) is elected leader at time t. Note that several nodes may be elected leaders at the same time steps.

A node \(P\) that is elected leader at time step \(t\) can extend a chain with a block that includes the solution \((P, t)\), the previous block’s hash \(h_{-1}\) and the transactions \(TXs\) to be confirmed. To verify that the block indeed came from \(P\), we require that the entire contents of the block i.e. \((h_{-1}, TXs, t, P)\) are signed under:math:P’s public key. The same as Nakamoto’s protocol, each node chooses the longest valid chain it has ever seen and extend the longest chain.

Note that the honest node’s only attempt to mine solutions of the form \((P, t)\), where \(t\) is the current time step, however the adversary may use incorrect block-times such as the time in the future or the time in the past. To prevent this kind of attacks from happening, we have the following additional restrictions on the block-times in a valid chain:

1. A valid chain must have strictly increasing block-times;
2. A valid chain cannot contain any block-times for the future;

We present our Sleepy consensus protocol as follows:

• On input init() from environment \(Z\):

  Generate (pk, sk), register pk with \(F_{CA}\), initialize

  \[chain := (\perp,\perp,time=0,\perp,\perp,h=0)\]

• On receive \(chain'\):

  If \(|chain'| > |chain|\) and \(chain'\) is valid and \(H(P,t) < D_p\) for valid \(P\) and \(t\), then \(chain := chain'\) and broadcast \(chain\).

• For every time step \(t\) and every honest node with party \(P\):

  • Receive transactions \(TXs\) from environment \(Z\).

  • If \(H(P, t) < D_p\) then let:

    \[ \begin{align}\begin{aligned}\delta := \verb|sign|(\verb|sk|, chain[-1].h, TXs, t)\\and\end{aligned}\end{align} \]
    \[ \begin{align}\begin{aligned}h' := hash(chain[-1].h,)\\Then let\end{aligned}\end{align} \]
    \[chain := chain || (chain[-1].h, TXs, t, P, \delta, h')\]

  • Output extract(chain) to \(Z\), where extract extract is the function outputs an ordered list containing the \(TXs\) extracted from each block in \(chain\).

Our protocol takes parameter \(p\) as input, where \(p\) is the probability each node is elected leader in a single time step. All nodes will invoke init function once it is spawned.

5. Simulator Components

In this section, we first introduce the overall structure of the simulator, then we introduce the three components of our simulator: Framework, Honest Party and Adversary Party. The last part of this section is the API document.

5.1. Structure

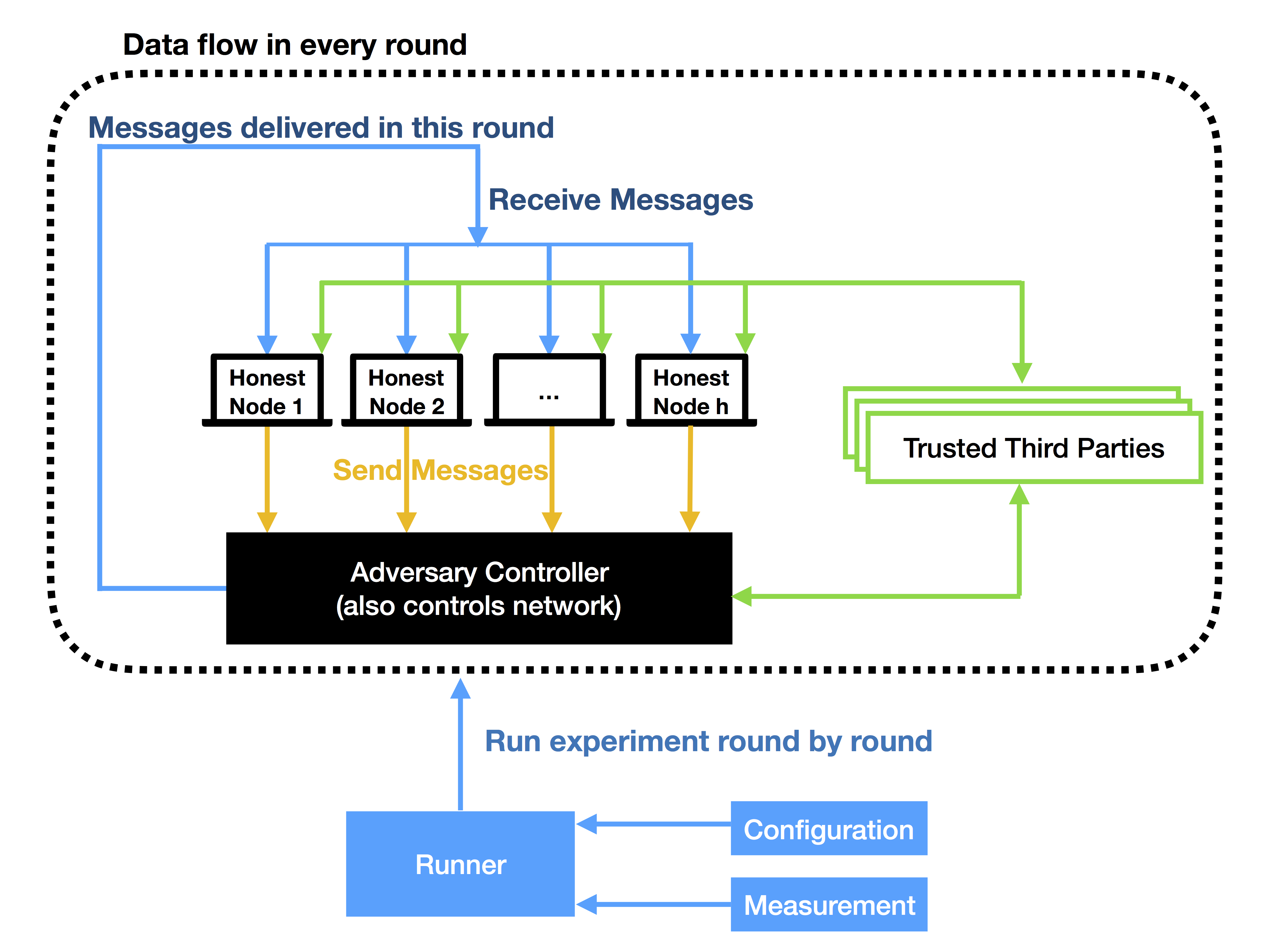
As shown in the figure, our simulator runs in a round-by-round style. The class framework.Runner controls the action in each round. By creating the subclasses of class framework.ConfigurationBase, user can configure the parameters(e.g. number of rounds, ratio of corrupted nodes) the run. Users can write subclasses of the class framework.MeasurementBase to provide the function of measuring the results(e.g. consistency and chain quality) of the experiment.

In each round, the adversary firstly delivers messages to the corresponding receivers. Then, the honest nodes send the messages to the adversary controller since the adversary has the control of the network. The class framework.Context provides a easy way for the honest nodes to interact with the network.

The class utils.FSignRSA and utils.FSignHash plays the role of trusted third party. User can also create the subclasses of class framework.TrustedThirdPartyBase.

5.2. Framework

Our framework implement several abstract classes for the users implement their own subclasses:

• class AdversaryControllerBase is the super class for the user defined adversary party.
• class ConfigurationBase is the super class for the user defined running configuration.
• class Context the network interface for the nodes to communicate with each other.
• class MeasurementBase is the super class for the user defined measurement.
• class NodeBase is the super class for the user defined node type.
• class Runner is the default round-by-round runner.
• class TrustedThirdPartyBase is the super class for the user defined trusted third party.

5.3. Honest Party

Each honest nodes has:

• node ID

• blockchain Since blockchain will fork, it’s actually a block tree. The longest chain is the main chain. According to Sleepy Consensus Protocol, the previous block should have smaller timestamp than the successor.

• transaction pool

  Receive transactions(tx) from network and store in tx pool temporarily. If the node receives a tx not in current tx pool, the node will forward(broadcast) this tx with its own signature immediately. At the end of each round, all txs remained in tx pool will form a new block append at the end of mainchain.
• orphan pool

  The node will receive blocks from the network. With the interference of Adv, some blocks will be delayed, but not lost. Perhaps some successive blocks have already received, but they can’t be connected to the block tree since they are waiting for their “father” block. So we need a “pool” to store those “orphan” block.

  The delete operation of a block in the orphan pool is very tricky. We only store single blocks, but we need to remove all successors of it at the same time, which results to a recursive process.
• probability

  probability is related to the mining difficulty \(D\). For node \(x\), if the hash value of its node ID and the current time is less than \(D\), then \(x\) is elected as the leader who has the right to mine a new block and broadcast to other nodes.

5.4. Adversary Party

We implement 2 kinds of adversaries in this project: Selfish Mining Attack and Consistency Attack.

5.4.1. Selfish Mining Attack

Ittay Eyal and Emin Gun Sirer [ES13] introduced the selfish mining attack, and Vitalik Buterin presented the adversary’s precise strategy here. In our project, we implement this attack method as sleepy.SelfishMining class and the corresponding measurement sleepy.ChainQualityMeasurement class.

5.5. Consistency Attack

We also implemented a naive consistency attack which is described as follows:

• Pick the longest chain from all honest chains and its private chain.

• For every honest message: delay by \(\Delta\).

• If adversary’s private chain is longer than the honest chain and it’s length is at least \(T + 1\), then it publish the chain and will break consistency.

• Here \(T\) is the security parameter, except with probability \(e^{-\Omega(T)}\):

  \(\forall\) honest chains \(chain^{r}_{i}\) and \(chain_{j}^{r'}\) s.t. \(r' \geq r\), \(chain_{i}^r[:\text{-T}] < chain_j^{r'}\)

• When the adversary has 60% of the computational power, he can keep developing his own private chain until honest chain is long enough, then release the chain to overwrite the last :math:` T ` blocks. So that the honest chain may be overwrite.

This attack method implemented in the class of sleepy.ConsistencyAttack.

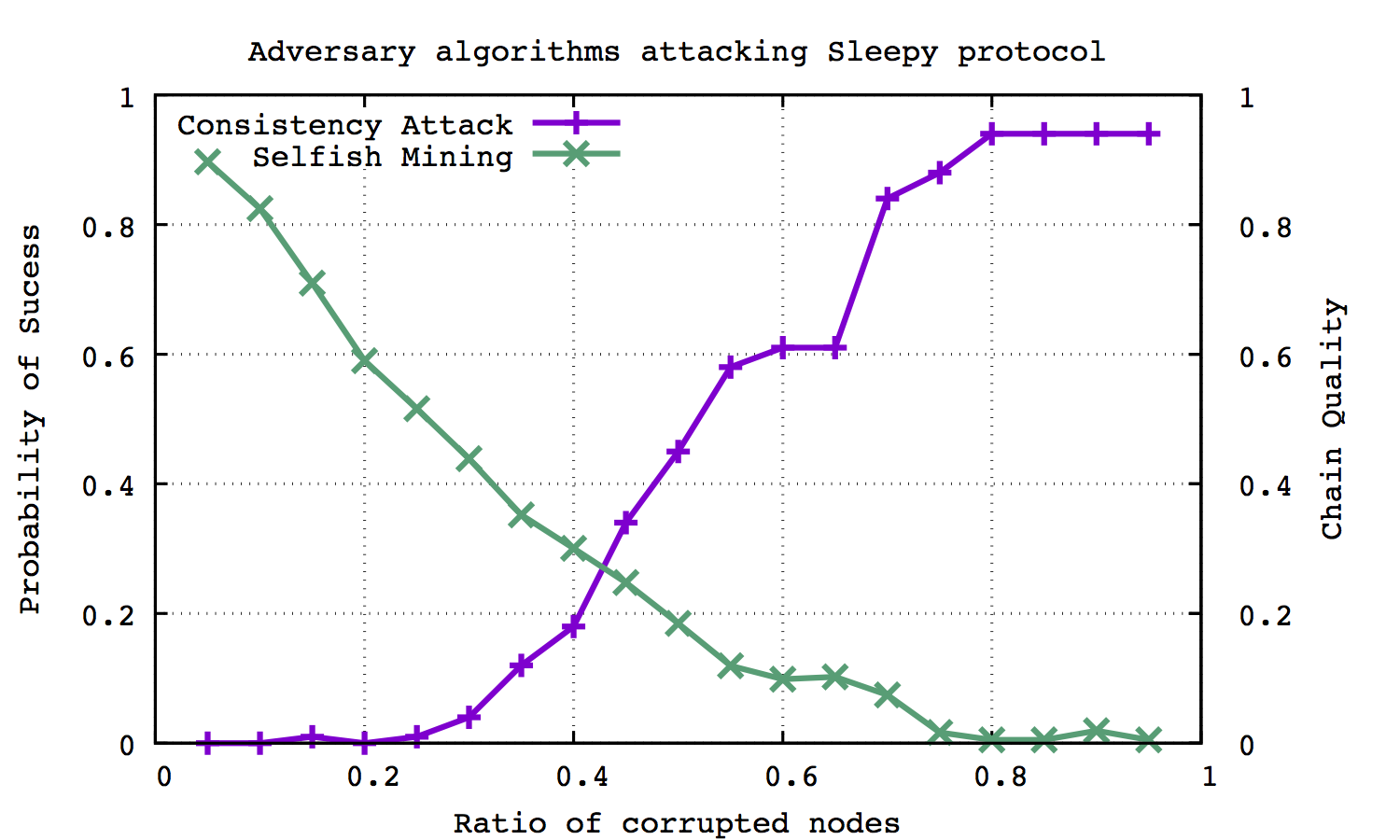
6. Experiment Results

For the 2 attacking methods, we implement several experiments on various sets of parameters. The following figure shows the relation between the probability of success and ratio of corrupted nodes for the naive consistency attack and the relation between chain quality between the ratio of corrupted nodes under the parameter setting of

\[n=20,\Delta = 2, T = 6, p = 0.05\]

7. Tutorial

This section contains a tutorial demonstrating how to implement a protocol and how to attack it in our framework. For more details, please refer to our source code in dcsim.dummy.

7.1. Description

The protocol we use here is easy to understand:

Supposing a scenario in which \(n\) people are voting for one of the two candidates(0/1), some of them are honest while the others are corrupt. Honest people have their own choice, and broadcast it. The final choice of an honest people is the majority of all people’s choices he/she receives. If all individuals are honest, they should reach a consensus.

What attackers do is to send 0 to honest people whose id is an odd number, and send 1 to honest people whose id is an even number.

7.2. Implementation

In class Configuration, we provide the interface for runner to get access to necessary information().

In class HonestNode, we simulate what honest people will do in function round_action(In this protocol, only two rounds are required: the first round to generate honest node’s own choice, the second round to gather all choice one receives).

In class DummyAttack, we implement our adversarial algorithm(which we discussed above) in function round_action.

In class Measurement, we set when to stop the simulation(2 rounds), and report the intermediate result after each round and eventually, report a final result(We say an attack is successful if and only if the consensus among honest people is broken).

In the main loop, we set different parameters and simulate the protocol by calling runner again and again:

runner = Runner(config)
runner.init()
res = runner.run()
results.append(res)

By averaging results, we get the estimation to the probability of successful attack.

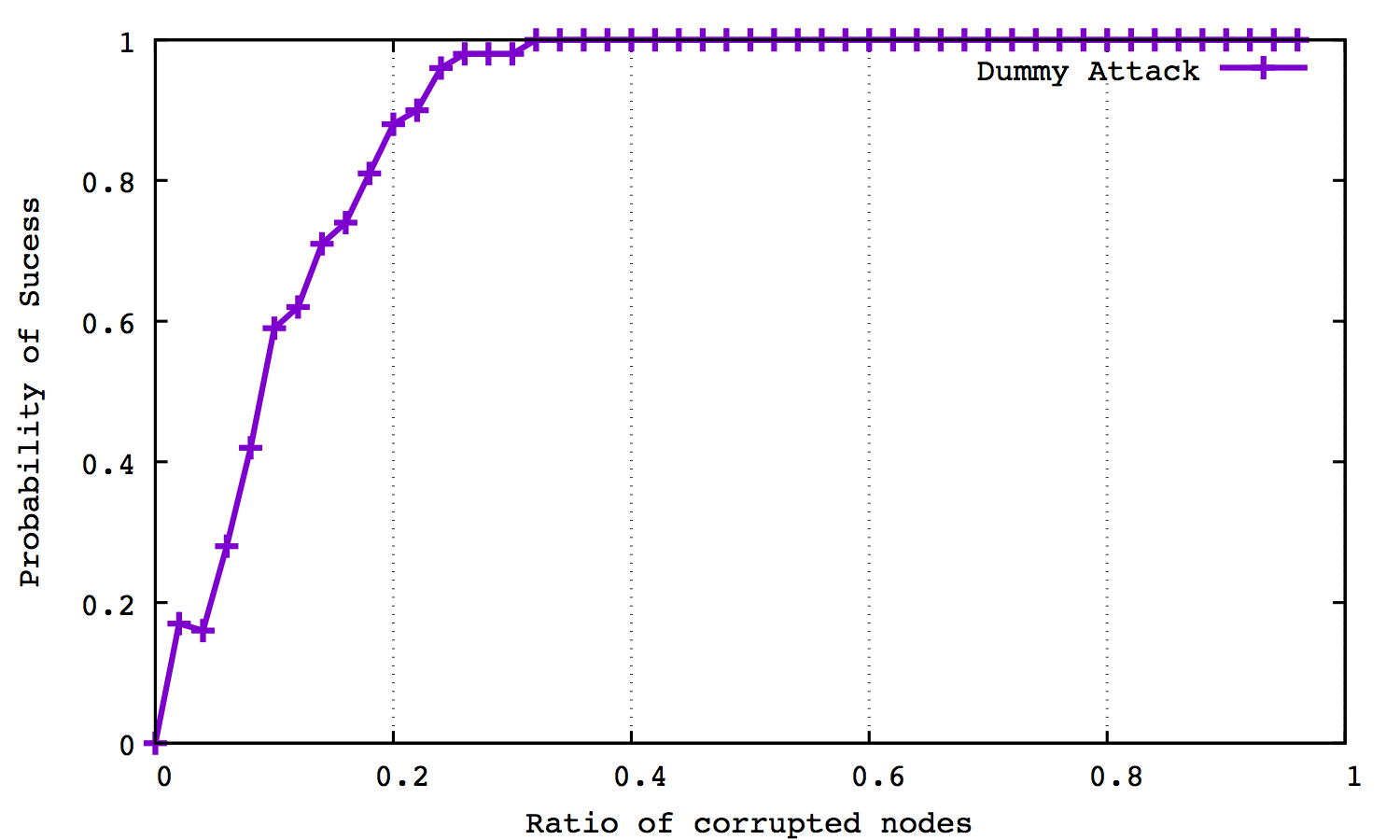
7.3. Result

In our experiment setting, we let \(n=50\), and use a group of different corrupt ratios(from \(\%2\) to \(\%96\), with interval \(\%2\)).

The figure below suggests how does the success rate grows as the corrupt node ratios increase.

8. Reference

[ES13]

Ittay Eyal and Emin Gün Sirer. Majority is not enough: bitcoin mining is vulnerable. CoRR, 2013. URL: http://arxiv.org/abs/1311.0243.

[PS16]

Rafael Pass and Elaine Shi. The sleepy model of consensus. Cryptology ePrint Archive, Report 2016/918, 2016. http://eprint.iacr.org/2016/918.